Wie im letzten Kapitel "Mit-/Ohne Zurücklegen" kennengelernt, kann ein Ereignis je nachdem was vorher passiert ist, mit unterschiedlichen Wahrscheinlichkeiten auftreten. Offenbar ist die Wahrscheinlichkeit für ein solches Ereignis abhängig vom Vorereignis - man nennt dies bedingte Wahrscheinlichkeit - sie gilt nur unter einer gewissen Bedingung.
Zieht man zum Beispiel ohne Zurücklegen eine zweite Karte aus einem Kartenspiel, so ist das Ereignis "Ass gezogen" unwahrscheinlicher, wenn man zuvor bereits eines der vier Asse gezogen hat.
Betrachten wir dazu noch einmal die zugehörigen Wahrscheinlichkeiten im Baumdiagramm:
Zwei Karten ohne Zurücklegen ziehen
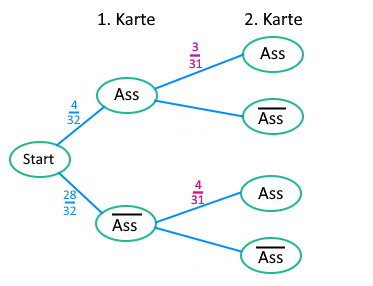
Wie man sieht, können wir auf die Frage "Wie groß ist die Wahrscheinlichkeit im zweiten Zug ein Ass zu ziehen" nicht direkt eine eindeutige Antwort geben. Wir können sie lediglich beantworten, indem wir die jeweilige Bedinung mit angeben:
Unter der Bedingung, dass wir im ersten Zug ein Ass gezogen haben, beträgt die Wahrscheinlichkeit für ein weiteres Ass \(\frac3{31}\).
Unter der Bedingung, dass wir im ersten Zug kein Ass gezogen haben, beträgt die WSK für ein Ass \(\frac4{31}\).
Um eine bedingte Wahrscheinlichkeit angeben zu können, muss man also auch die Bedingung aufschreiben. Die mathematische Notation lautet \(P_{\text{Bedingung}}(\text{Ereignis})\) - man schreibt die Bedingung also als Index an die Wahrscheinlichkeit.
In unserem Beispiel
\(P_{\text{Ass im ersten Zug}}(\text{Ass im zweiten Zug})=\frac3{31}\)
\(P_{\text{kein Ass im ersten Zug}}(\text{Ass im zweiten Zug})=\frac4{31}\)
Bedingte Wahrscheinlichkeit
\(P_{\text{Bedingung}}(\text{Ereignis})\)
Im Baumdiagramm stehen die bedingten Wahrscheinlichkeiten immer an den hinteren Ästen, denn hier stellt man sich ja gerade die Frage, wie groß die Wahrscheinlichkeit für ein zweites Ereignis ist, wenn das erste Ereignis bereits in einer bestimmten Weise aufgetreten ist. Ein allgemeines Baumdiagramm mit bedingten Wahrscheinlichkeiten sieht also wie folgt aus:
Zufallsversuch mit den Ereignissen A und B
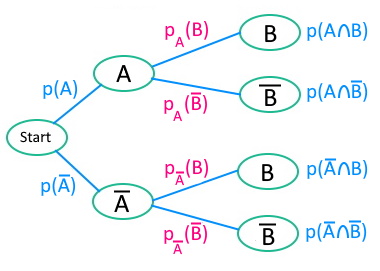
Die bedingten Wahrscheinlichkeiten stehen an den Ästen zur zweiten Versuchsstufe und sind in pink dargestellt.
Betrachten wir davon den obersten Ast: Hier steht die Wahrscheinlichkeit für das Ereignis B - allerdings unter der Bedingung, dass A bereits eingetroffen ist.
Am dritten Ast steht wiederum die Wahrscheinlichkeit für das Ereignis B - hier jedoch unter der Bedingung, dass A zuvor nicht eingetroffen ist.
Man darf die bedingten Wahrscheinlichkeiten dabei nicht mit den Schnittwahrscheinlichkeiten ganz am Ende des Baumes verwechseln! Etwa beschreibt \(p(A\cap{B})\) ganz am Ende des oberen Astes die Wahrscheinlichkeit, dass sowohl A als auch B (ohne irgendwelcher Bedingungen) eintritt.
Zum Verständnis - und um gleichzeitig einen sehr wichtigen Satz zu bedingten Wahrscheinlichkeiten herzuleiten - üben wir das Erstellen eines solchen Baumdiagramms mit bedingten Wahrscheinlichkeiten an einem Beispiel.
Hilft Basketball beim Abitur?
An einer Schule bestehen 80% das Abitur. Von den erfolgreichen Abiturienten haben 45% während der Abiturphase aktiv Basketball gespielt. Desweiteren haben 16% des Abiturjahrgangs weder das Abitur bestanden, noch in dieser Zeit Basketball gespielt.
Fertige ein Baumdiagramm an und nimm Stellung zur oben genannten Aussage.
Abitur dank Basketball?
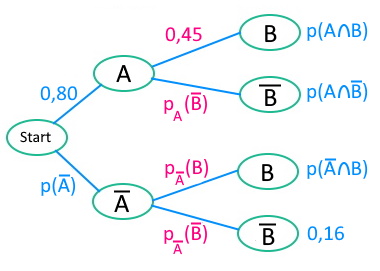
Schritt 1
Wir bezeichnen mit A das Ereignis "Abitur bestanden" und mit B "Basketball gespielt".
Im Baumdiagramm links sind die Angaben aus dem Text bereits eingetragen.
\(p(A)=80\%\)
Da 80% das Abitur bestehen, ist das die Wahrscheinlichkeit für das Ereignis A.
\(p_{A}(B)=45\%\)
Im Text steht, dass 45% der erfolgreichen Abiturienten Basketball spielen - die angegebene Wahrscheinlichkeit stimmt also nur unter der Bedingung, dass es sich um einen erfolgreichen Abiturienten handelt.
\(p(\overline{A}\cap\overline{B})=16\%\)
Bei 16% der Schüler sind beide Ereignisse erfüllt. Beachte, dass dies keine bedingte Wahrscheinlichkeit ist. Bedingte Wahrscheinlichkeiten beziehen sich immer nur auf einen Teil der Ausgangsmenge, zum Beispiel "von den erfolglosen Abiturienten haben 16% kein Basketball gespielt". Die 16% beziehen sich aber auf alle Schüler - sie gelten ohne irgendeiner Bedingung.
zu Schritt 2
Der Satz von Bayes
\(p_{\text{ Bedingung}}(\text{Ereignis})=\frac{p(\text{Bedingung }\cap\text{ Ereignis})}{p(\text{Bedingung})}\)
Um bedingte Wahrscheinlichkeiten zu berechnen, muss man also die Schnittwahrscheinlichkeit von der Bedingung und dem Ereignis durch die Wahrscheinlichkeit der Bedingung teilen.
So gesehen, beschreibt der Satz von Bayes die umgekehrte erste Pfadregel.
Also dann - vervollständigen wir unser Baumdiagramm zu den Basketballspielenden Abiturienten:
Abitur dank Basketball? | Teil 2
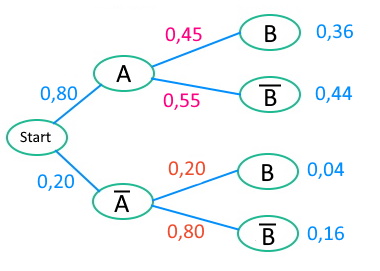
Wir berechnen die beiden fehlenden bedingten Wahrscheinlichkeiten also mit Hilfe des Satz von Bayes:
\(p_{\overline{A}}(B)=\frac{0,04}{0,2}=0,2\)
\(p_{\overline{A}}(\overline{B})=\frac{0,16}{0,2}=0,8\)
So weit so gut - das Baumdiagramm ist fertig. Stimmt denn jetzt die Aussage, dass Basketballspieler eine höhere Wahrscheinlichkeit für ein erfolgreiches Abitur haben?!
Um das zu beantworten, bräuchten wir die Wahrscheinlichkeit, dass ein Basketballer sein Abitur besteht - wir suchen \(p_B(A)\). Und da es sich um eine bedingte Wahrscheinlichkeit handelt, berechnen wir sie mit dem Satz von Bayes:
\(p_B(A)=\frac{p(B\cap{A})}{p_B}\)
\(p(B\cap{A})\) können wir direkt aus dem Baum ablesen, sie beträgt \(p(B\cap{A})=p(A\cap{B})=0,36\).
Für \(p(B)\) müssen wir nach zweiter Pfadregel noch die zugehörigen Schnittwahrscheinlichkeiten zusammenrechnen, denn die Basketballspieler sind sowohl in \(p(A\cap{B})\), als auch in \(p(\overline{A}\cap{B})\) enthalten - ergo ist
\(p(B)=0,36+0,04=0,4\).
Die gesuchte WSK beträgt nach Satz von Bayes also \(p_B(A)=\frac{0,36}{0,4}=0,9\)
es bestehen also 90% aller Basketballspielenden Schüler das Abitur.
Zum Vergleich bestimmen wir das noch für die anderen Schüler:
\(p_{\overline{B}}(A)=\frac{0,44}{0,6}\approx0,733\).
Hier sind es also nur ca. 73%. Also tatsächlich - Basketballspieler haben in diesem Versuch eine höhere Chance auf ein erfolgreiches Abitur!
Das umgedrehte Baumdiagramm
Wie in der Basketball-Aufgabe zu sehen, können wir aus unserem Baumdiagramm nicht alle bedingten Wahrscheinlichkeiten des Versuchs ablesen. Da unser Baum zuerst das Ereignis A angibt, finden wir entsprechend nur die bedingten Wahrscheinlichkeiten, die \(A\) oder \(\overline{A}\) als Bedingung haben.
Für die restlichen bedingten Wahrscheinlichkeiten (mit \(B\) und \(\overline{B}\) als Bedingung) benötigen wir den umgekehrten Baum, müssen also ein Baumdiagramm erstellen, das zuerst das Ereignis B unterscheidet.
Bei Aufgaben zu bedingten Wahrscheinlichkeiten ist es ratsam, einfach immer direkt beide Bäume anzufertigen - zum einen können wir dann ohne weiterer Rechnung stets alle Fragen beantworten (da wir mit beiden Bäumen alle Wahrscheinlichkeiten kennen), zum anderen kann die Aufgabe auch so fies gestellt sein, dass man sogar beide Bäume zeichnen muss!
Dazu ein Beispiel:
Bei einer Umfrage zur Handynutzung sind 60% der Versuchsteilnehmer weiblich. Von den Frauen geben 90% an, mindestens einmal am Tag ein Handy zu nutzen. 14% aller Teilnehmer benutzen ihr Handy hingegen seltener.
Fertige zu diesem Zufallsversuch beide Baumdiagramme an!
Frauen und Handys | Eintragen der gegebenen WSKs
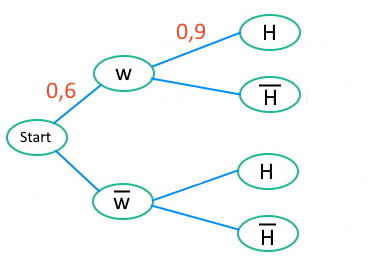
\(p(w)=60\%\)
Es sind 60% aller Teilnehmer weiblich, ergo ist das \(p(w)\).
\(p_w(H)=90\%\)
90% der Frauen (also unter der Bedingung "Frau") nutzen ein Handy. Wir tragen diese bedingte Wahrscheinlichkeit also beim Ast von w zu H ein.
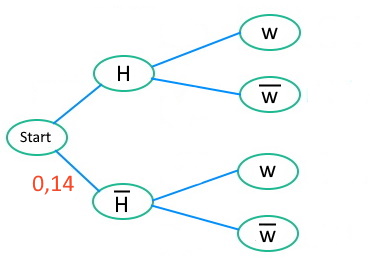
\(p(\overline{H})=14\%\)
Die 14% beziehen sich wieder auf alle Teilnehmer (es handelt sich also nicht um eine bedingte Wahrscheinlichkeit). Wir tragen sie im umgekehrten Baum an den Ast der Nicht-Handynutzer ein.
Frauen und Handys | Eintragen bekannter Gegenwahrscheinlichkeiten
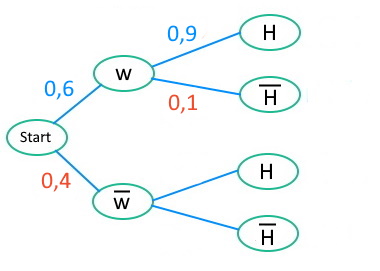
Durch die bereits eingetragenen Wahrscheinlichkeiten können wir jeweils die Gegenwahrscheinlichkeiten angeben:
Wenn 60% weiblich sind, sind 40% männlich.
Wenn 90% der Frauen ein Handy nutzen, nutzen 10% der Frauen kein Handy.
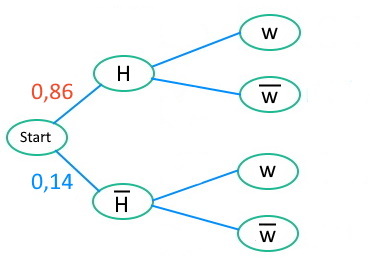
Wenn 14% aller Teilnehmer kein Handy nutzen, tun es 86% der Teilnehmer schon.
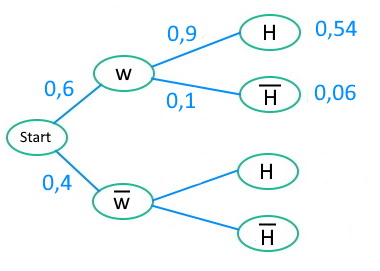
Frauen und Handys | Nutzen der 1. Pfadregel
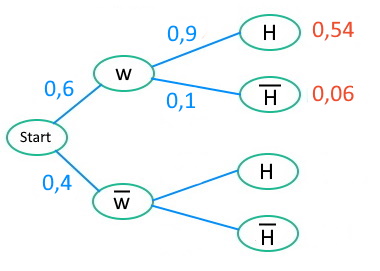
Mit Hilfe der ersten Pfadregel können wir im oberen Baum die ersten beiden Schnittwahrscheinlichkeiten ausrechnen:
\(p(w\cap{H})=0,6\cdot0,9=0,54\)
\(p(w\cap\overline{H})=0,6\cdot0,1=0,06\)
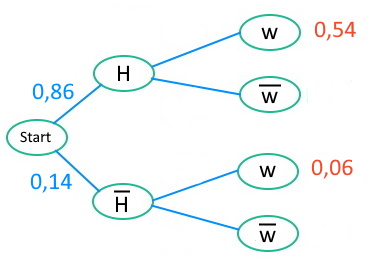
Diese beiden Wahrscheinlichkeiten können wir auch in den umgekehrten Baum (aber Vorsicht: an anderer Stelle!) eintragen.
Frauen und Handys | Nutzen des Satz von Bayes
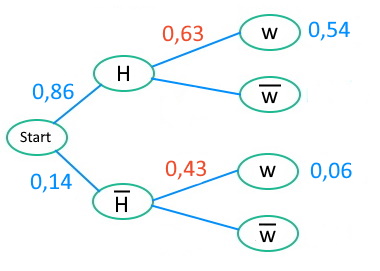
Im unteren Baum können wir nun mit Hilfe des Satz von Bayes zwei bedingte Wahrscheinlichkeiten ausrechnen, da wir die benötigten Wahrscheinlichkeiten kennen.
\(p_H(w)=\frac{0,54}{0,86}\approx0,63\)
\(p_{\overline{H}}(w)=\frac{0,06}{0,14}\approx0,43\)
Frauen und Handys | Gegenwahrscheinlichkeiten und 1. Pfadregel
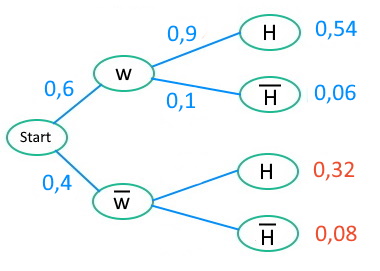
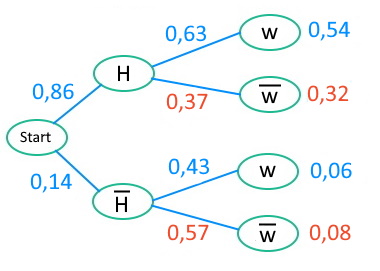
Jetzt können wir die Gegenwahrscheinlichkeiten der gerade berechneten bedingten Wahrscheinlichkeiten im unteren Baum bestimmen.
Wenn 63% der Handynutzer weiblich sind, dann sind 37% von ihnen männlich.
Genauso: 43% der Handymuffel sind weiblich, ergo sind 57% männlich.
Jetzt können wir auch die zugehörigen Schnittwahrscheinlichkeiten ausrechnen, nämlich:
\(p(H\cap\overline{w})=0,86\cdot0,37=0,32\)
\(p(\overline{H}\cap\overline{w})=0,14\cdot0,57=0,08\)
Diese tragen wir auch direkt in den oberen Baum ein. Und da wir jetzt alle Schnittwahrscheinlichkeiten bestimmt haben, können wir kurz kontrollieren, ob tatsächlich 100% herauskommen:
\(0,54+0,06+0,32+0,08=1\)
Es stimmt alles!
Frauen und Handys | Ein letztes mal Bayes...
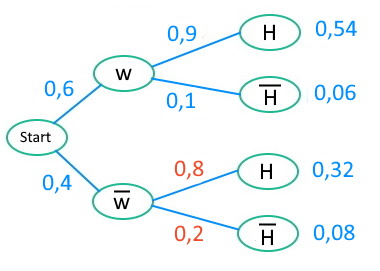
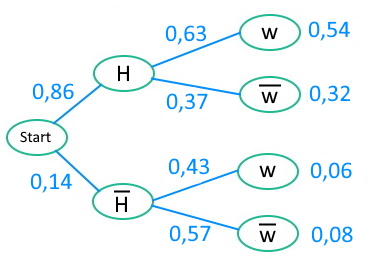
Die beiden letzten bedingten Wahrscheinlichkeiten des oberen Baums bestimmen wir wieder mit Bayes:
\(p_{\overline{w}}(H)=\frac{0,32}{0,4}=0,8\)
Obwohl wir es dann jetzt doch einfacher finden, die Gegenwahrscheinlichkeit \(p_{\overline{w}}(\overline{H})=0,2\) anzugeben.
Zusammenfassung Bedingte Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten werden mit dem "Satz von Bayes" berechnet, er lautet
\(p_{\text{Bed}}(E)=\frac{p(\text{Bed}\cap{E})}{p(\text{Bed})}\)
Am besten zeichnet man bei Aufgaben zu bedingten Wahrscheinlichkeiten immer einfach beide Bäume (und berechnet die bedingten Wahrscheinlichkeiten durch umgedrehte 1. Pfadregel) - denn aus ihnen lassen sich immer alle bedingten Wahrscheinlichkeiten ablesen.
Stochastik & Statistik